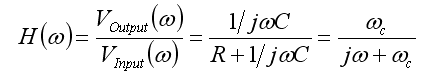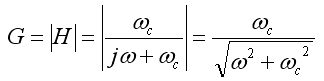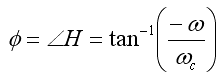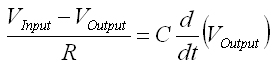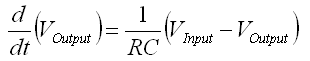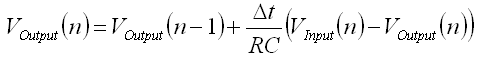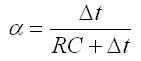High-Pass Filter
Low-Pass Filter
Numerical Low-Pass Filter
High-Pass RC Filter:
-
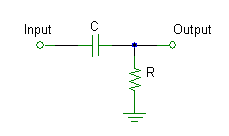
- Capacitor passes high frequencies, blocks low
frequencies
- In frequency domain, capacitor impedance,
Z(ω)=1/jωc
- So, the impulse response,
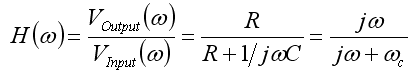
- where,
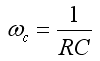
- Whose magnitude,
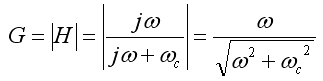
- And phase,
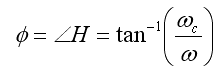
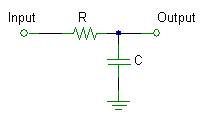
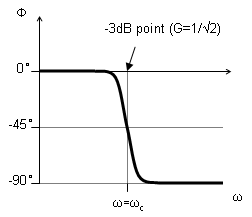
- So that,
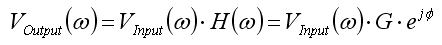
- G is easiest viewed on a Bode (log-log) plot:
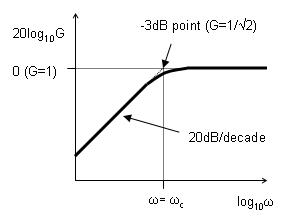
- Φ is 0° for high frequencies, 90° at low
frequencies, and 45° at the -3dB point:
- Note: The affect of a high-pass filter can be numerically
undone with the droop correction algorithm.
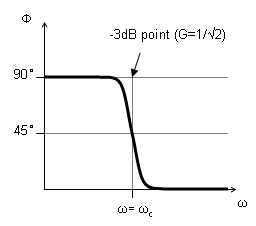
- Low-Pass
RC Filter:
 Capacitor
passes high frequencies, blocks low frequencies
Capacitor
passes high frequencies, blocks low frequencies- In frequency domain, capacitor impedance,
Z(ω)=1/jωc
- So, the impulse response,
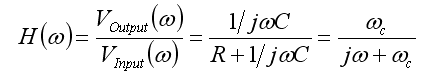
- where,
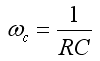
- Whose magnitude,
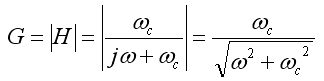
- And phase,
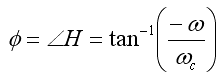
- So that,
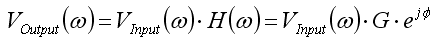
- G is easiest viewed on a Bode (log-log)
plot:
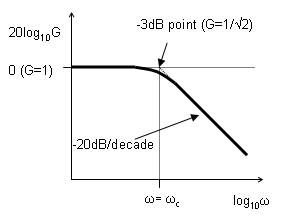
- Φ is 0° for high frequencies, 90° at low
frequencies, and 45° at the -3dB point:
Copyright © Raymond Allen
2006-2021

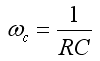
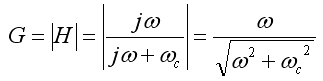
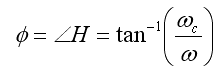
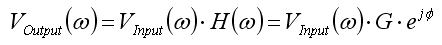


 Capacitor
passes high frequencies, blocks low frequencies
Capacitor
passes high frequencies, blocks low frequencies