Definitions of contrast and diagram below from "The Physics of Medical X-Ray Imaging", 2nd Ed Author: Bruce H. Hasegawa, Ph.D..   Note also that the sign of the contrast is usually ignored.

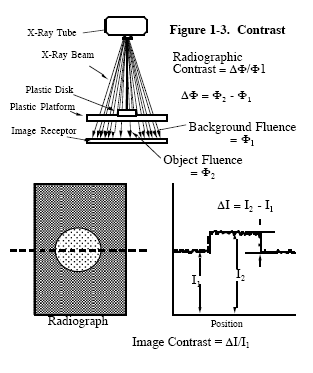
	In this case, F is proportional to f(x), so that F1 corresponds to f(0) and F2 to f(w*(1+Mph)), assuming that the slits are resolved.
	The image contrast cannot be determined without knowing the proportionality constant between F and OD of the film.
	It can be shown that the three equal max. values on film occur at x=0, ±2w*(1+Mph) and the two equal min. values at x=±w*(1+Mph), assuming the slits are resolved.
	If the slits are not resolved the film profile will appear as two peaks (or even one) instead of the expected three.
	The slit pitch equals 1/(2*w) and is usually expressed in line-pairs per millimeter.
	The radiographic magnification equals 1+m.
	Since the source is a disk, the line spread function is a circular:  l(x)=sqrt(r^2-x^2) for |x|<r and 0 otherwise and r=D/2.
	The edge spread function is the integral of the line spread function:  e(x)=x*sqrt(r^2-x^2)+r^2*arcsin(x/r)+r^2*pi/2.
	The resultant on the film plane is f(x)=e((w/2)*(1+m)-x) -e((-w/2)*(1+m)-x) +e((3w/2)*(1+m)-x) -e((5w/2)*(1+m)-x) +e((-3w/2)*(1+m)-x) -e((-5w/2)*(1+m)-x).